In part 1 I dove into Spotify Codes and explained the general technical concepts of how they work. If you haven’t read that post you should check it out. I shared it on reddit where it generated a lot of interesting discussion. Ludvig Strigeus, a key early developer at Spotify and the person who invented Spotify Codes, even stopped by and shared some more information on their creation and the rationale behind them!
At the end of part 1 I wrote that I wasn’t sure about some of the details, so I was not able to implement my own barcode to URI converter. Thanks to a little more digging and a lot of help from someone on Stack Overflow I can now do that conversion.
This article is going to be a little bit more technical than part 1 as I try to explain exactly how Spotify encodes their barcodes. I will include some more resources if you want to keep learning.
Encoding a URI into a Spotify Barcode
I find it easier to understand Spotify Barcodes by starting with the URI and working through the encoding process.
Media reference
A media reference is first generated by Spotify for a Spotify URI. The media reference is what gets encoded into the barcode and links the barcode to the URI. Spotify maintains a database of media reference to URI mappings. Media references let Spotify track which codes are scanned, enable them to theoretically re-map codes, and just look better when encoded. If Spotify encoded a whole URI, it would look something like this (and would be harder to scan):

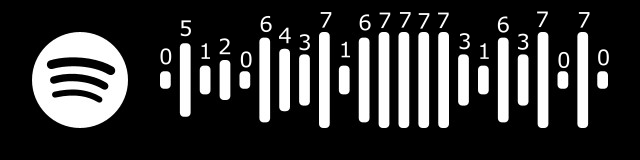
Let’s start with the media reference 57639171874 which points to the following playlist: spotify:user:spotify:playlist:37i9dQZF1DWZq91oLsHZvy (Indie x Running).
The media reference can be expressed as a 37 bit binary number:
57639171874 -> 0100010011101111111100011101011010110
CRC Calculation
Next, cyclic redundancy check bits are calculated for the media reference. A CRC calculates check bits to verify the integrity of the data. (Tangent: another simple checksum algorithm we use every day to validate credit card numbers is the Luhn algorithm.)
Spotify uses CRC-8 with the following generator:
x^8 + x^2 + x + 1
Which gives us the following polynomial when fully written out:
1x^8 + 0x^7 + 0x^6 + 0x^5 + 0x^4 + 0x^3 + 1x^2 + x + 1
[1, 0, 0, 0, 0, 0, 1, 1, 1]
The CRC is calculated by following these steps:
- Pad with 3 bits on the right
01000100 11101111 11110001 11010110 10110000
- Reverse bytes
00100010 11110111 10001111 01101011 00001101
- Calculate CRC as normal (highest order degree on the left)
11001100
- Reverse CRC
00110011
- Invert check
11001100
- Finally append to step 1 result
01000100 11101111 11110001 11010110 10110110 01100
|----------Media Ref--------------------||--CRC--|
Here is a simple version of a crc calculator (step 3):
def crc(data, polynomial):
# xor the data with the polynomial at each occurrence of
# a 1 in the data. Return the remainder as the checksum.
n = len(polynomial) - 1
initial_length = len(data)
check_bits = data + [0] * n
for i in range(initial_length):
if check_bits[i] == 1:
for j, p in enumerate(polynomial):
check_bits[i + j] = check_bits[i + j] ^ p
return check_bits[-n:]
We can use the check bits to verify that the contents of the data match what was intended by the “sender”:
def check_crc(data, polynomial, check_bits):
full_data = data + check_bits
for i in range(len(data)):
if full_data[i] == 1:
for j, p in enumerate(polynomial):
full_data[i + j] = full_data[i + j] ^ p
return 1 not in full_data
data = [0,0,1,0,0,0,1,0,1,1,1,1,0,1,1,1,1,0,0,0,1,1,1,1,0,1,1,0,1,0,1,1,0,0,0,0,1,1,0,1]
check = [1,1,0,0,1,1,0,0]
poly = [1,0,0,0,0,0,1,1,1]
print(check_crc(data, poly, check))
# True
Convolutional encoding
These 45 bits are then convolutionally encoded. Convolutional codes add redundancy to data to make it possible to decode the data if errors are introduced during transmission. I recommend you check out these MIT lecture notes to learn more about convolutional codes.
Spotify’s patent is not very clear on what convolutional encoding is performed:
The code can then be transformed into an error correcting code, such as a forward error correcting code. The forward error correction used can, for example, be a convolutional code.
However, “Doyle” on Stack Overflow identified that Spotify uses the following generator polynomials:
g0 = 1011011
g1 = 1111001
The generator polynomial represents which bits of the input should be XOR’ed together in a sliding window.
Tail biting
Before we start calculating the parity bits, we must prepend stream with last 6 bits of data:
01000100 11101111 11110001 11010110 10110110 01100
|-----|
001100 01000100 11101111 11110001 11010110 10110110 01100
|----|
Another approach would be to prepend 0s to the input, but Spotify chose to go with this tail-biting method.
Encoding
We can focus on one generator at a time. Below is a step by step walkthrough of how the parity bits are generated for g0. I reversed the polynomial because it is easier to display right to left in the example.
Bit #0
001100010001001110111111110001110101101011011001100
1101101 <- generator polynomial (mask)
-------
0001000 = 1 (xor the bits together)
Bit #1
001100010001001110111111110001110101101011011001100
1101101 <- generator polynomial (mask)
-------
0100001 = 0 (xor the bits together)
Bit #2
001100010001001110111111110001110101101011011001100
1101101 <- generator polynomial (mask)
-------
1100000 = 0 (xor the bits together)
Bit #3
001100010001001110111111110001110101101011011001100
1101101 <- generator polynomial (mask)
-------
1000100 = 0 (xor the bits together)
Bit #4
001100010001001110111111110001110101101011011001100
1101101 <- generator polynomial (mask)
-------
0001000 = 1 (xor the bits together)
Continue this to the end of the stream of input bits:
Bit #45
001100010001001110111111110001110101101011011001100
1101101 <- generator polynomial (mask)
-------
1001100 = 1 (xor the bits together)
The result of encoding with the first generator, g0:
100011100111110100110011110100000010001001011
The result of encoding with g1:
110011100010110110110100101101011100110011011
Here is a (naive) algorithm for calculating the parity bits:
def encode(bits: List[int], polynomial: List[int], tail_bite=False):
"""Convolutionally encode the stream of bits using the generator polynomial.
If tail_bite == True, prepend the tail of the input. Otherwise use 0s to fill.
"""
if tail_bite:
tail = bits[-(len(polynomial) - 1):]
else:
tail = [0 for i in range(len(polynomial) - 1)]
full = tail + bits
polynomial.reverse() # Reverse since we're working the other direction
parity_bits = []
for i in range(len(bits)):
parity = 0
for j in range(len(polynomial)):
parity ^= full[i + j] * polynomial[j]
parity_bits.append(parity)
return parity_bits
These two parity bit sequences are then interleaved (abab…):
1 0 0 0 1 1 1 0 0 1 1 1 1 1 0 1 0 0 1 1 0 0 1 1 1 1 0 1 0 0 0 0 0 0 1 0 0 0 1 0 0 1 0 1 1
1 1 0 0 1 1 1 0 0 0 1 0 1 1 0 1 1 0 1 1 0 1 0 0 1 0 1 1 0 1 0 1 1 1 0 0 1 1 0 0 1 1 0 1 1
result:
110100001111110000101110111100110100111100011010111001110001000101011000010110000111001111
Puncturing
At this point we have gone from 45 bits to 90 bits. The rate of this convolutional code is 1/2 (one input bit results in 2 parity bits).
A rate of 1/2 is actually somewhat low for this application (see this article about QR code rates). The rate can be increased by “puncturing” the code. We can remove every third bit to increase the rate to 3/4:
110100001111110000101110111100110100111100011010111001110001000101011000010110000111001111
11 10 00 11 11 00 10 11 11 10 11 10 11 10 01 01 11 00 11 00 00 10 01 00 01 11 00 11 00 11
result:
111000111100101111101110111001011100110000100100011100110011
This is equivalent to puncturing the two parity bit sequences with the patterns 101 and 110 before interleaving. Puncturing is a nice, simple way to increase the rate of your code after you estimate the frequency of expected errors.
Permutation
Spotify then shuffles the data to spread out errors when a whole bar is lost:
A shuffling process may be used to spread out the potential errors (e.g., if a whole bar/distance is missing). Instead of having the encoded bar lengths be consecutive, the lost bits are non-consecutive in the code word. This improves the chances for the forward error correction to work when a whole bar or distance is lost. Thus to scan the optical code, after the lengths of the found bars are converted into bits with certainties, the bits are shuffled back into the right order.
The bits are permuted by choosing every 7th bit (modulo 60) from the input.
def permute(bits, step=7):
for i in range(len(bits)):
yield bits[(i * step) % len(bits)]
Input and result:
111000111100101111101110111001011100110000100100011100110011
111100110001110101101000011110010110101100111111101000111000
Map to bar heights
Finally, map the bits to bar heights between 0 and 7 using gray code:
| Decimal | Binary | Gray |
|---|---|---|
| 0 | 000 | 000 |
| 1 | 001 | 001 |
| 2 | 010 | 011 |
| 3 | 011 | 010 |
| 4 | 100 | 110 |
| 5 | 101 | 111 |
| 6 | 110 | 101 |
| 7 | 111 | 100 |
111 100 110 001 110 101 101 000 011 110 010 110 101 100 111 111 101 000 111 000
5 7 4 1 4 6 6 0 2 4 3 4 6 7 5 5 6 0 7 0
Three additional bars are added as reference points at the start, end, and 12th position:
[0]5741466024[7]3467556070[0]
Which gives us the resulting Spotify code:

Decoding
Let’s reiterate why we went through the process of calculating the CRC and convolutionally encoding the data:
- Convolutional codes allow us to correct for errors in a message by sending “redundant” bits with the message
- The CRC lets the client check the validity of the decoded Spotify code. If the check bits are not correct, the client can scan the code again. When they are correct, then the client can ping Spotify’s servers. As Ludvig says, “I chose to include a CRC to let the client have a way to more easily discard invalid codes without a backend roundtrip.”
The process of transforming an image of a Spotify code to a media reference follows approximately the same steps as encoding in reverse. However, there is a good bit of theory around decoding a convolutional code.
Convolutional decoding
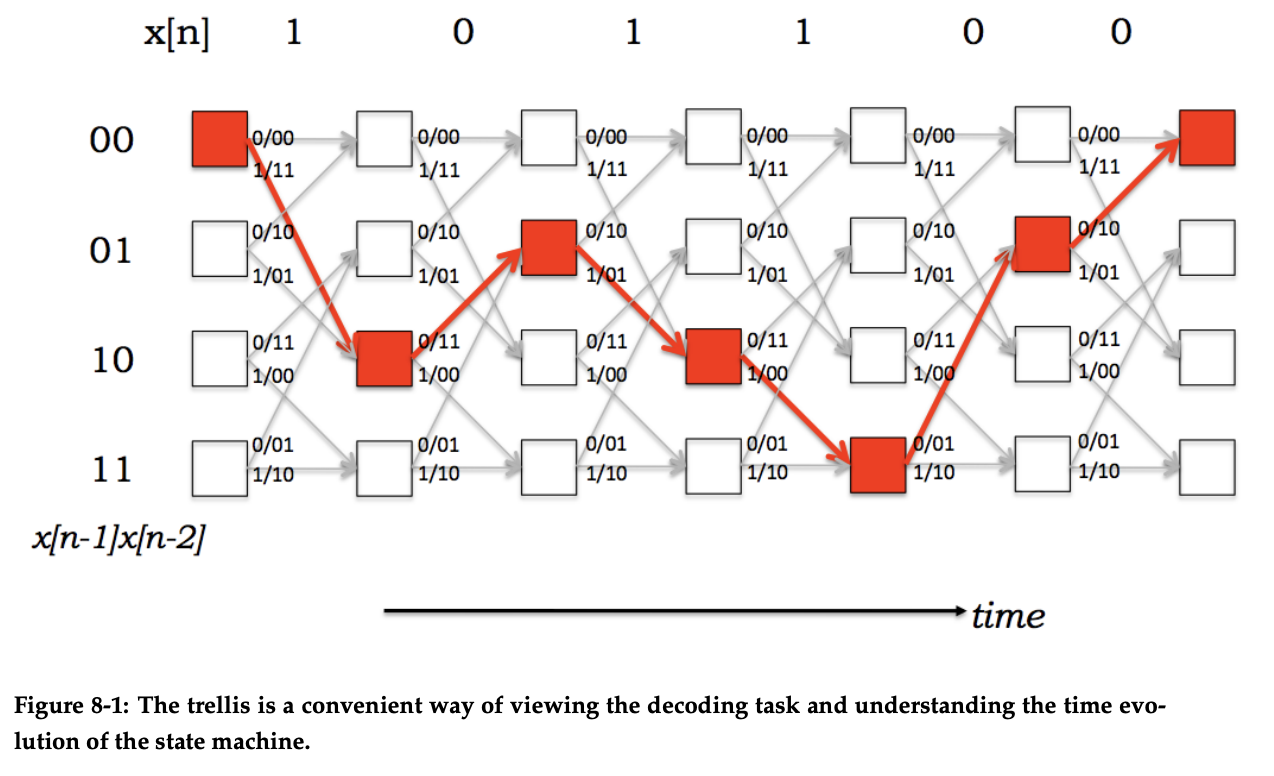
A deep dive into the various algorithms used to decode a convolutional code is beyond the scope of this article. However, I’d highly recommend you check out these MIT lecture notes on the Viterbi algorithm to learn more about one of these algorithms. Briefly, the algorithm provides a way of determining the most likely original sequence from the parity bit streams. This trellis diagram is a visual representation of the algorithm - finding the path with the least number of errors through the parity bit streams.
Working solution
If you’d like to see a working decoder, you can check out the code here. You will need to get your personal access token from Spotify because the code has to ping their media_ref -> uri look-up server. The code utilizes Doyle’s linear algebra solution, so if you are into that you can check that out.
I validated this solution on a few more Spotify codes:

heights: [0, 6, 6, 0, 7, 6, 0, 2, 2, 3, 1, 7, 0, 7, 6, 4, 6, 1, 4, 7, 4, 1, 0]
media ref: 26560102031
uri: spotify:track:1ykrctzPhcSS9GS3aHdtMt

heights: [0, 2, 6, 7, 1, 7, 0, 0, 0, 0, 4, 7, 1, 7, 3, 4, 2, 7, 5, 6, 5, 6, 0]
uri: spotify:user:jimmylavallin:playlist:2hXLRTDrNa4rG1XyM0ngT1
media ref: 67775490487

heights: [0, 5, 7, 4, 1, 4, 6, 6, 0, 2, 4, 7, 3, 4, 6, 7, 5, 5, 6, 0, 5, 0, 0]
uri: spotify:user:spotify:playlist:37i9dQZF1DWZq91oLsHZvy
media ref: 57639171874
standard forward dynamic programming solution to maximum-likelihood decoding of a discrete-time, finite-state dynamical system observed in memoryless noise
I had to laugh at a sentence I came across in an article about the Viterbi Algorithm:
Shortly afterward, in a paper submitted in May 1968 [23], Jim Omura observed that the VA [Viterbi Algorithm] was simply the standard forward dynamic programming solution to maximum-likelihood decoding of a discrete-time, finite-state dynamical system observed in memoryless noise.
I’m not sure about you, but I would not describe “the standard forward dynamic programming solution to maximum-likelihood decoding of a discrete-time, finite-state dynamical system observed in memoryless noise” with the word “simple”.
My goal for this article was to try to explain the Spotify Codes encoding process in an approachable way. If you have any questions please reach out and ask for clarification!
Further Reading
Reed-Solomon Codes and the Exploration of the Solar System
High-Rate Punctured Convolutional Codes for Soft Decision Viterbi Decoding
Viterbi Decoding of Convolutional Codes
Convolutional codes (MIT lecture notes)
Punctured Convolutional Encoding
Performance of concatenated codes for deep space missions
Convolutional Codes and State Machine View/Trellis (MIT Slides)
The Error Correcting Codes Page